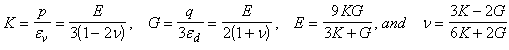
Definition of elastic parameters

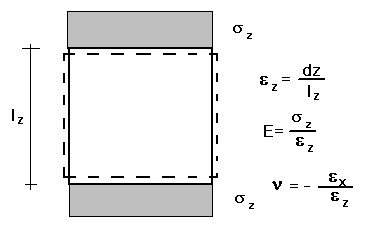
Subjecting a cube to a uniform stress in the direction z (vertical), sz, as shown in the figure below, will result in a change in length of the sides. When the deformations are very small compared to the dimensions of the cube the strains will be equal to the relative change of length.

Elastic parameters for uniaxial stress.

If the material is linear elastic, then the ratio of vertical stress, sz, to vertical strain, ez, will be a constant, the coefficient of elasticity or Young’s modulus (E). This is known as Hooke’s law. The ratio between the horizontal strain (ex or ey) and the vertical strain is also a constant. The ratio will be negative, and the positive value is known as Poisson’s ratio (n). A stress in one direction is seen to produce a strain proportional to -n/E in a perpendicular direction.

A shear stress, txz = tzx, will produce a shear strain, gxz = gzx. If the material is isotropic, the constant shear modulus, G, will be:

The shear strain does not affect the normal strains.

For three-dimensional loading of an isotropic material Hooke’s law may be written by the above equation for G and by:

with rotation of the subscripts. For the general anisotropic case E, n, and G should take the same subscript as the corresponding stress, and strain for n.

Because few pavement materials are ideally elastic it is often useful to divide the stress into a hydrostatic and a deviatoric component.

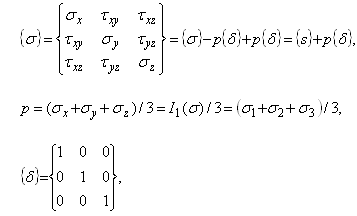
I1(s) is the first stress invariant (independent of the orientation of the co-ordinate system), p is the mean normal stress or the hydrostatic pressure, and {s} is the deviator stress tensor. The mean deviator stress is derived from the second deviator stress invariant:

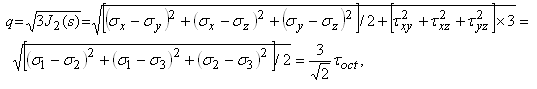
where toct is the octahedral shear stress.

The strains used with p and q are the volumetric and deviator strain:

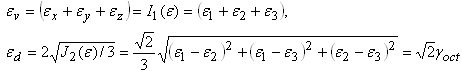
where goct is the octahedral shear strain.

The ratio of hydrostatic stress to volumetric strain is called the bulk modulus, K = p/ev. The relationships between K, G, E and n are: