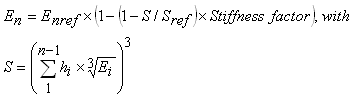
Unbound materials

During calibration of the CalME models it was found that the moduli of unbound materials could vary with the stiffness of the asphalt layers. This could happen both when the variation in stiffness was due to temperature variations and when it was due to fatigue damage to the asphalt. For the granular layers the change in stiffness was the opposite of what would be expected due to the non-linearity of the material. To describe this stiffness variation of the unbound layers the following relationship is used:

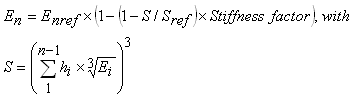
Equation: Modulus of unbound material as a function of confinement or bending stiffness.

where hi is the thickness of layer i,

 Enref is the modulus of layer n at a bending stiffness S = Sref,

and Sref and Stiffness factor are constants.

If full slip has developed between two or more layers their combined stiffness is found from:

For partial slip between layers a linear interpolation is done between full and no slip.

The unbound layers for some of the Heavy Vehicle Simulator (HVS) tests also showed typical non-linearity, with the modulus of granular layers increasing with increasing bulk stress and the modulus of cohesive materials decreasing with increasing deviator stress. Because of the variation in modulus given by the equation for confinement (bending stiffness) these non-linearities had to be treated as functions of the wheel load rather than as functions of the stress condition:

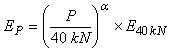
Modulus of unbound material as a function of wheel load.

where EP is the modulus at wheel load P in kN,

 E40 kN is the modulus at a wheel load of 40 kN, and

 α is a constant (positive for granular materials and negative for cohesive).

If a constant tire radius is used in the response calculations (to speed up the calculations) the moduli are only adjusted to the standard wheel loads (20 kN for single wheels and 40 kN for dual wheels).

The modulus may also be affected by moisture ingress. As the modulus of the asphalt decreases due to micro- and macro-cracking, the material may become permeable. If the moduli of the asphalt layers all have decreased to a certain fraction of the initial modulus, given as an input value, the modulus of the unbound layer may be divided by a value, also given as an input for the unbound material (see Incremental Recursive form, Custom.

For effects of seasonal variations see Seasonal effects on unbound materials.

For AC on PCC the k-value of the layers below the PCC layer is determined from the surface deflection under a standard load of 40 kN. The deflection is calculated using elastic layer theory and the k-value, that will produce the same deflection, is determined through iteration, using Westergaard's equation.